[ML]Self-Attention

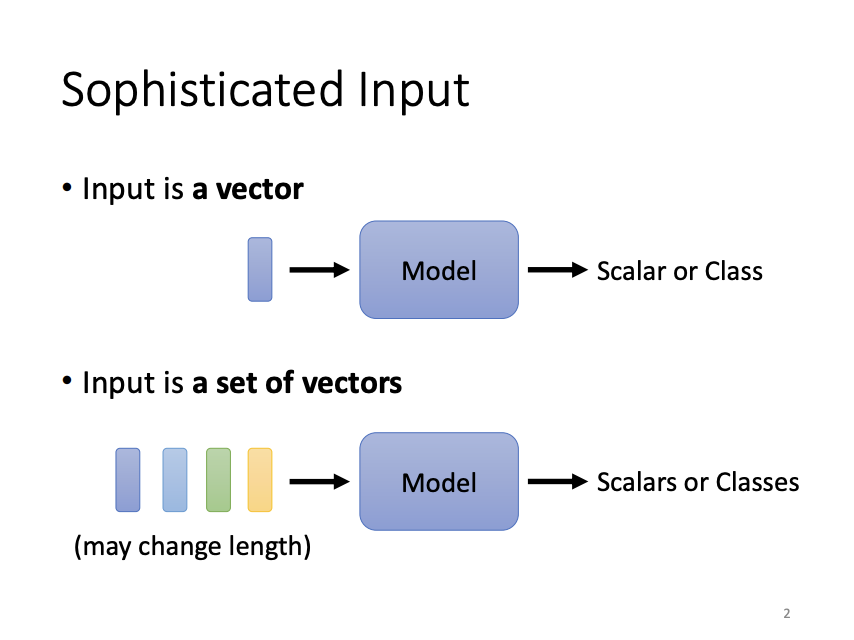
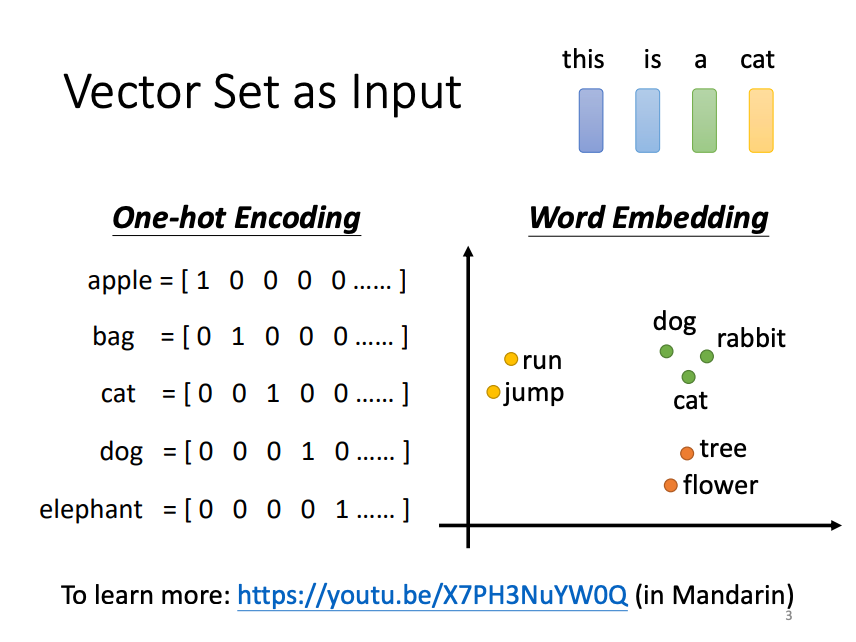
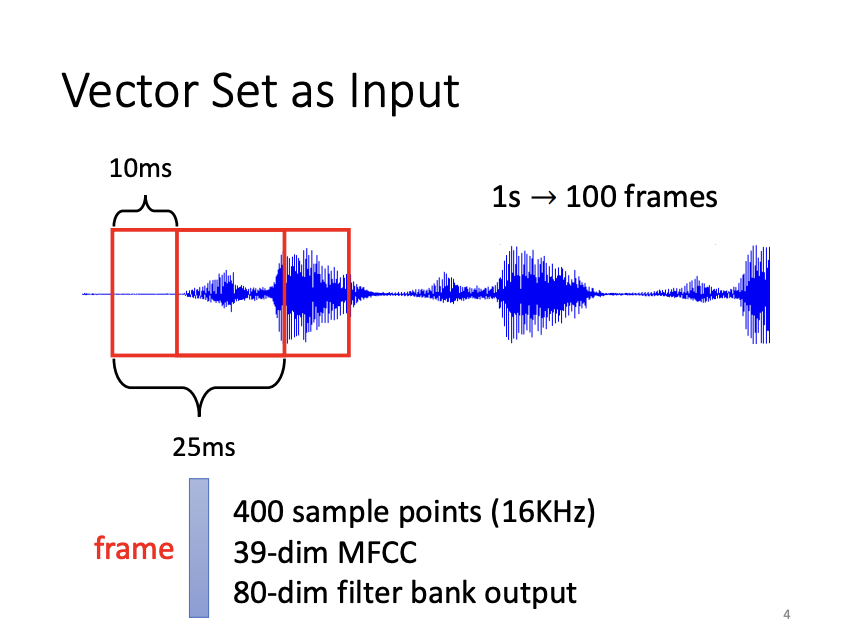
In machine learning models, the form of input can vary. It is not always a fixed-length vector, sometimes, it may be a set of vectors with varying lengths. For instance, in natural language processing, each word is often represented as a vector, and a sentence is treated as a sequence of such vectors. Similarly, in audio processing, a continuous audio signal is segmented into frames, each of which is represented as a vector.

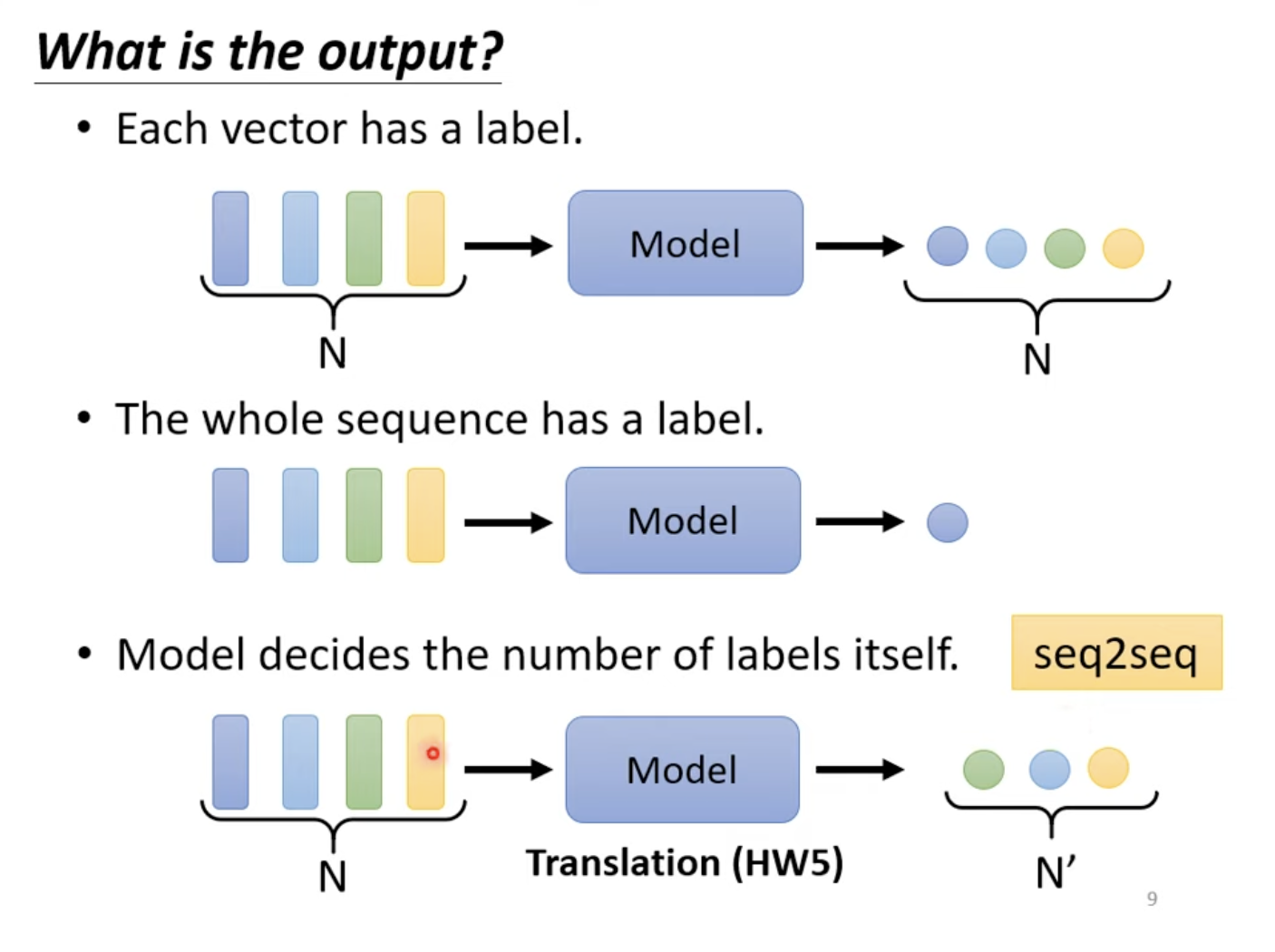
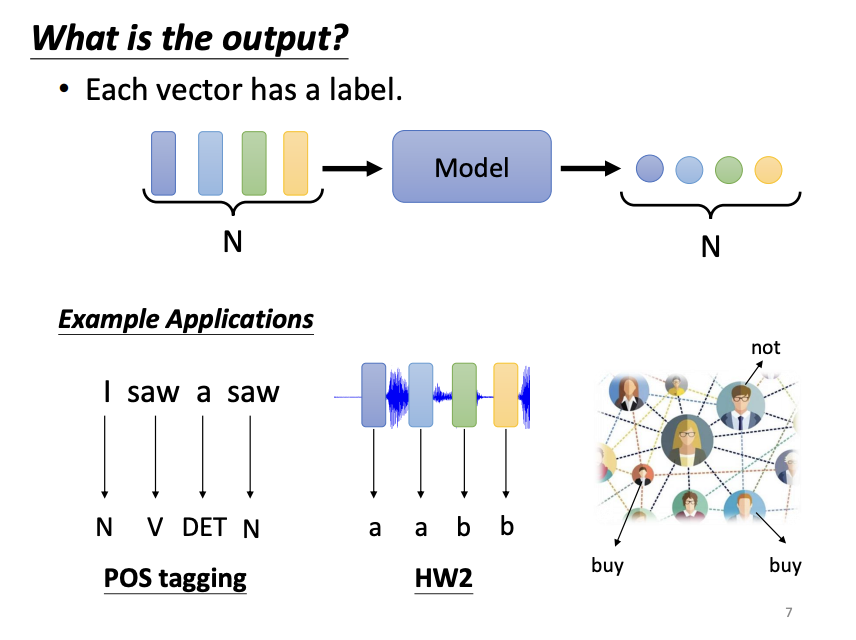
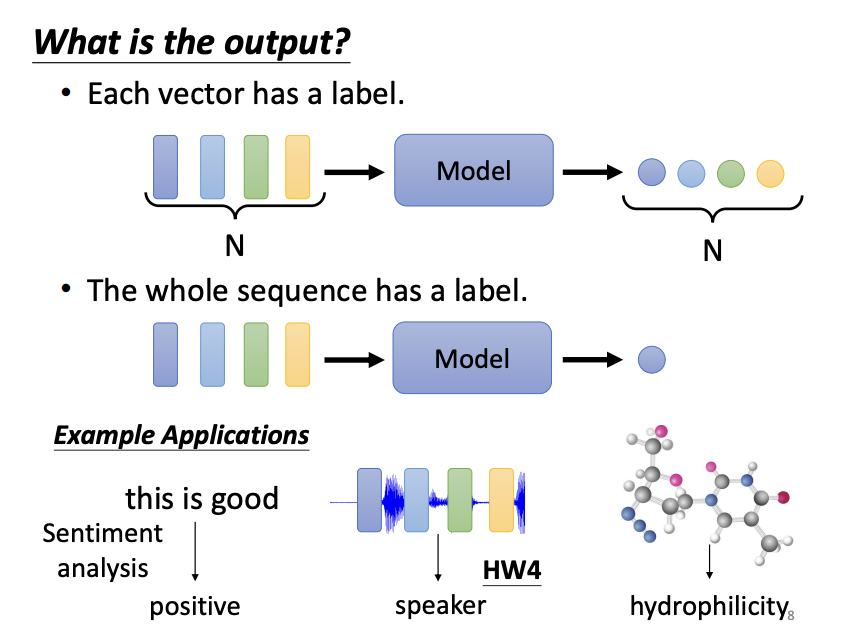
Likewise, the form of the output can differ depending on the task. In some cases, the model outputs the same number of labels as the input vectors (sequence labeling), as seen in tasks like part-of-speech (POS) tagging, where each word in a sentence receives a tag. In other cases, the model generates a single label for an entire sequence of vectors, such as in sentiment analysis, where the model determines whether the sentiment of a sentence is positive or negative, or in speaker recognition. Further more, in sequence-to-sequence (seq2seq) tasks, like machine translation, the model determines the number of output labels dynamically.

Sequence Labeling

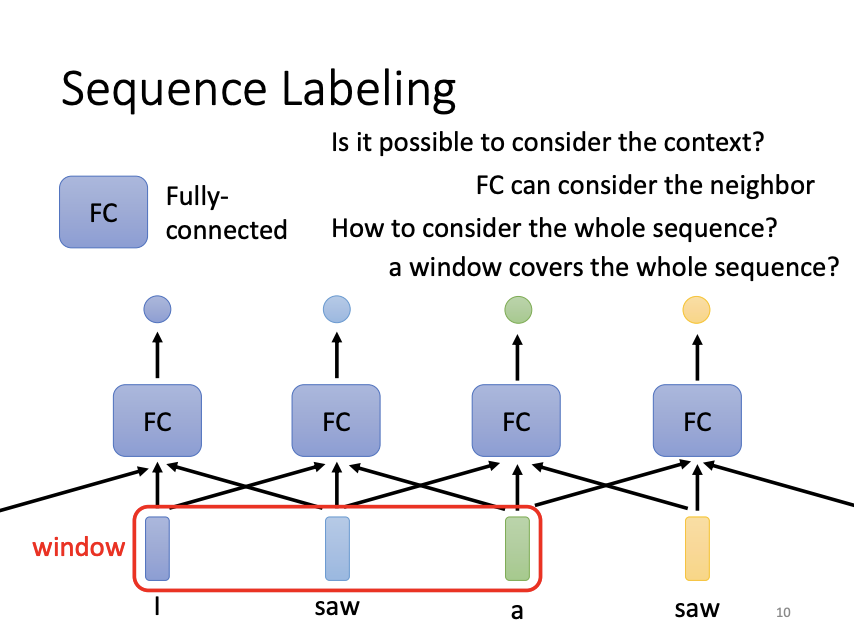
For sequence labeling tasks, fully connected networks often fail to capture dependencies between vectors, as they treat each input vector independently. While sliding windows can capture local dependencies by considering nearby vectors, this approach is limited because it cannot adapt to sequences of varying lengths. Moreover, using a window large enough to cover all input vectors may lead to inefficient models with a large number of parameters. To address these limitations, self-attention mechanisms are introduced.

Self-Attention Mechanism

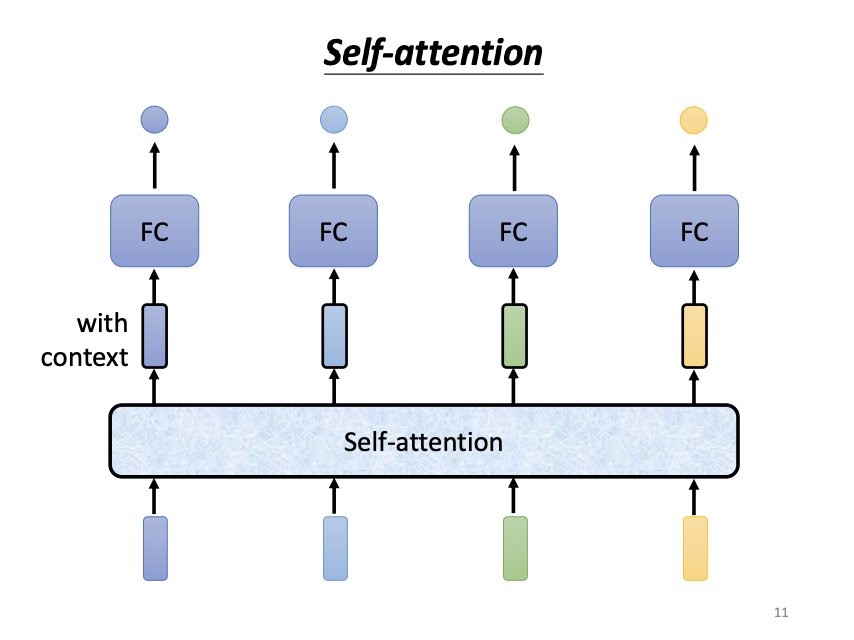
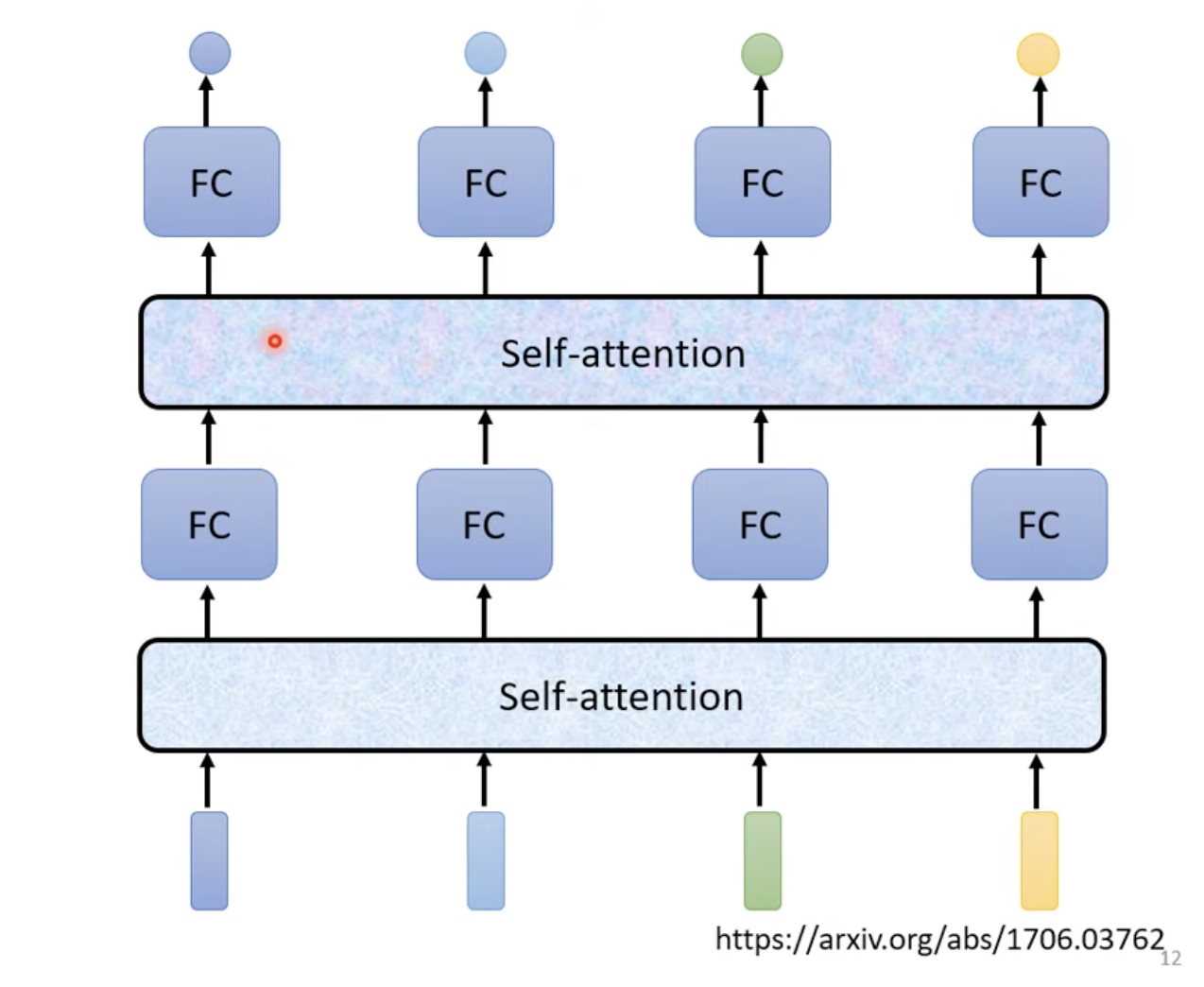
The self-attention mechanism processes all input vectors in a sequence simultaneously, outputting the same number of context-aware vectors. For each input vector, self-attention produces a new vector that incorporates information from the entire sequence before passing it to a fully connected network. Importantly, self-attention can be applied multiple times, often interleaved with fully connected layers, to enhance the representation of the input.

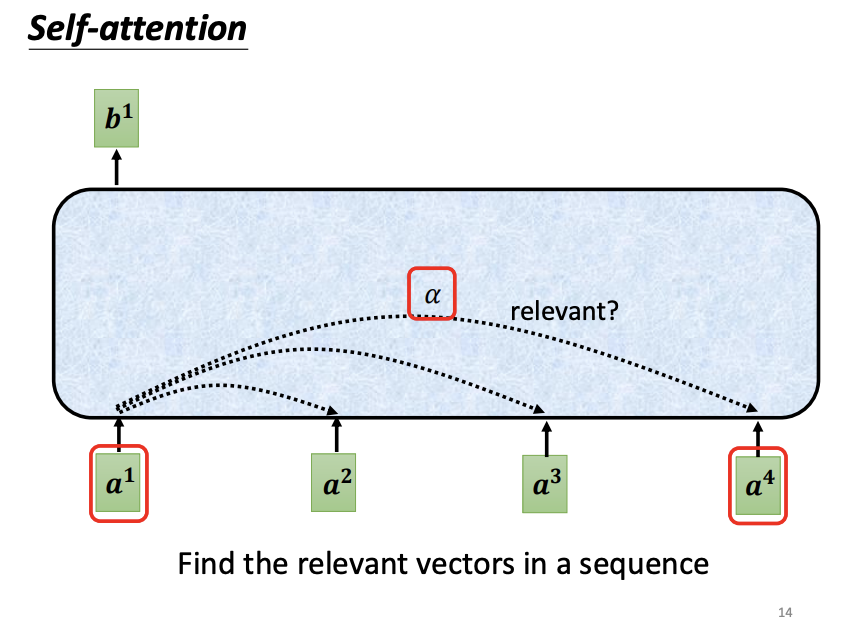
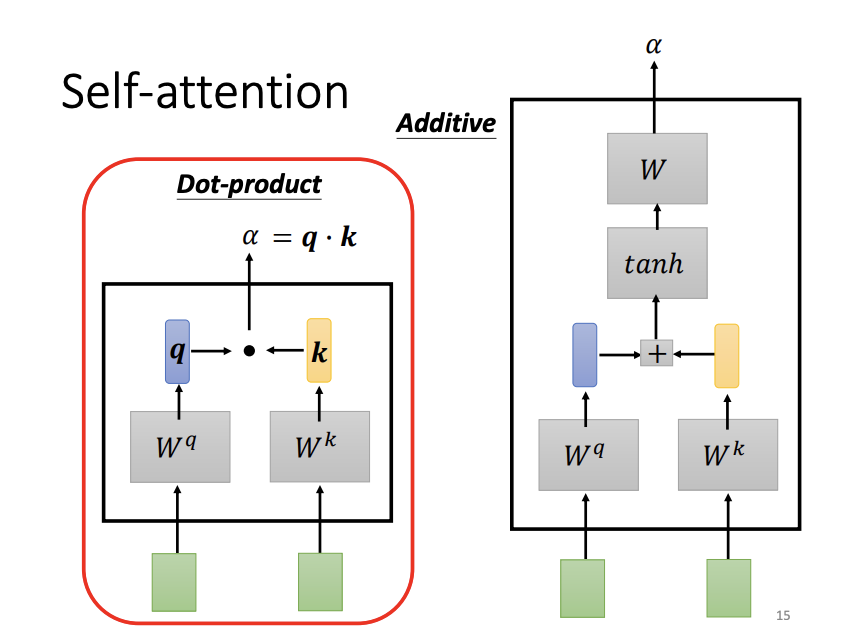
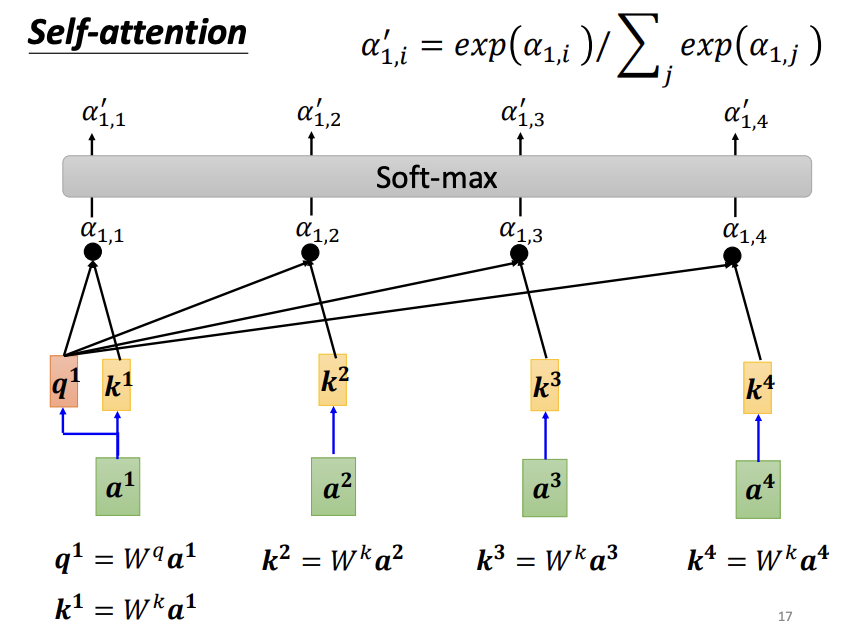
To compute the output vectors, self-attention calculates the relevance between each input vector and all other input vectors. One common method to quantify this relevance is the dot-product. In this approach, the input vectors are multiplied by two separate matrices: the query matrix and the key matrix. The dot-product between the resulting query and key vectors yields an attention score, which indicates the relevance between the two input vectors. Another approach to measuring relevance is the additive method.

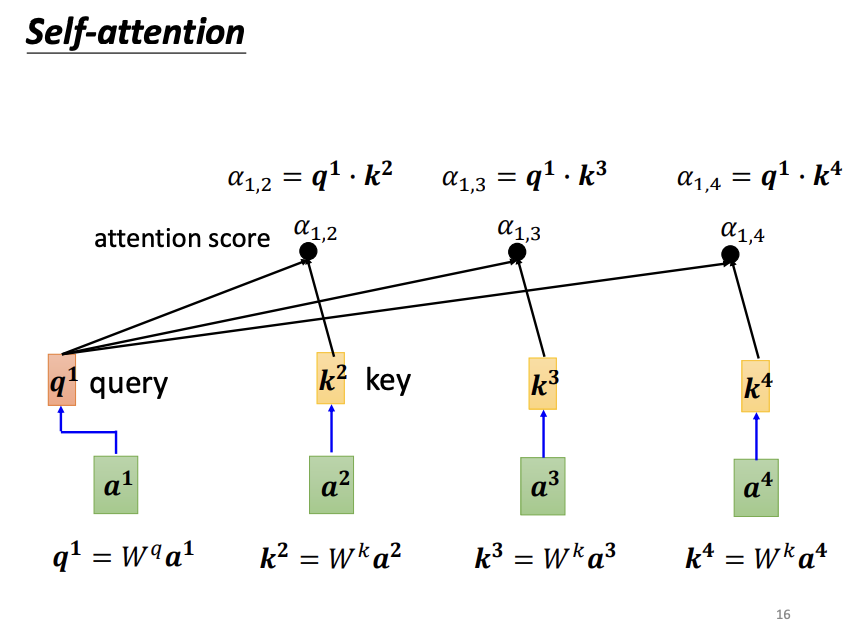
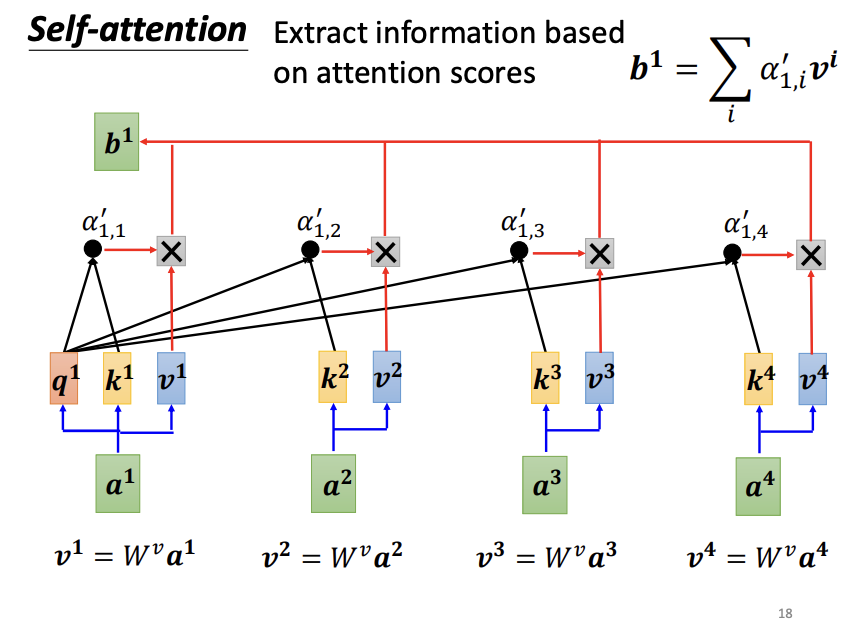
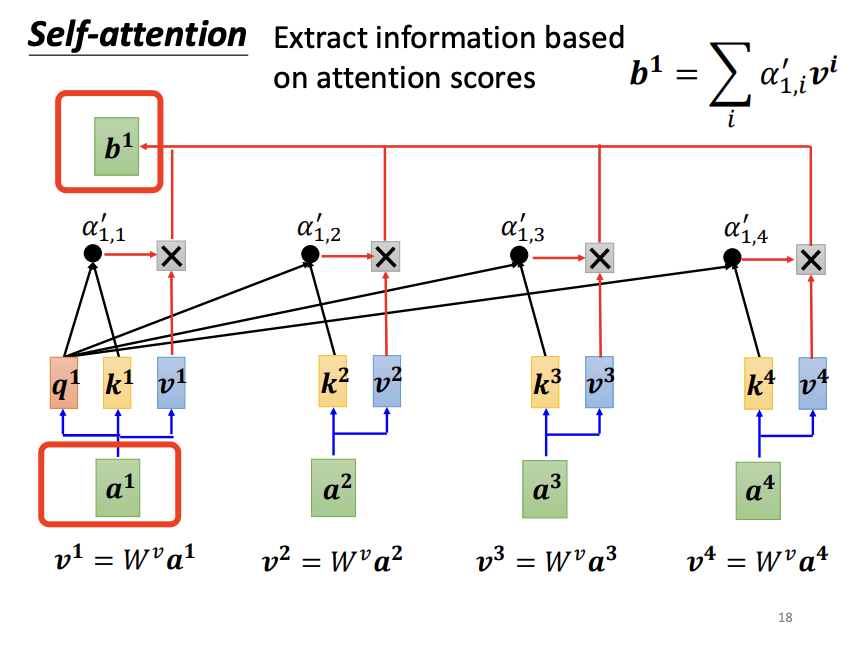
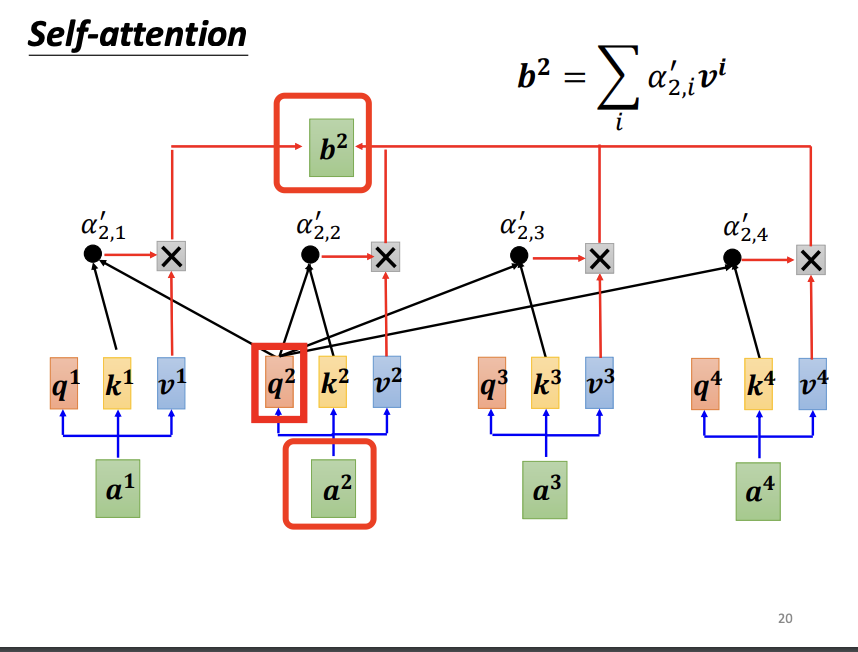
For each input vector, the self-attention mechanism evaluates its relevance to all other input vectors using the dot-product approach. Specifically, for a given input vector, a query matrix is applied to generate a query vector, while a key matrix is applied to the remaining input vectors to generate corresponding key vectors. The dot-product between the query vector and each key vector produces an attention score, which quantifies the relevance between the two vectors. Notably, an input vector also computes its relevance with itself. After calculating all attention scores, an activation function, such as softmax or ReLU, is typically applied for normalization. With these normalized attention scores, a value matrix (v matrix) is introduced to extract information from the input vectors. Each input vector is multiplied by the value matrix to produce a value vector, and the attention scores are then used to weight these value vectors. The weighted value vectors are summed to form the final output vector. If an input vector is highly relevant to others, it will have a greater influence on the resulting output vector.

Each input vector undergoes the same process described above. Since the computation of each output vector is independent of the others, these vectors can be calculated in parallel, significantly improving computational efficiency.

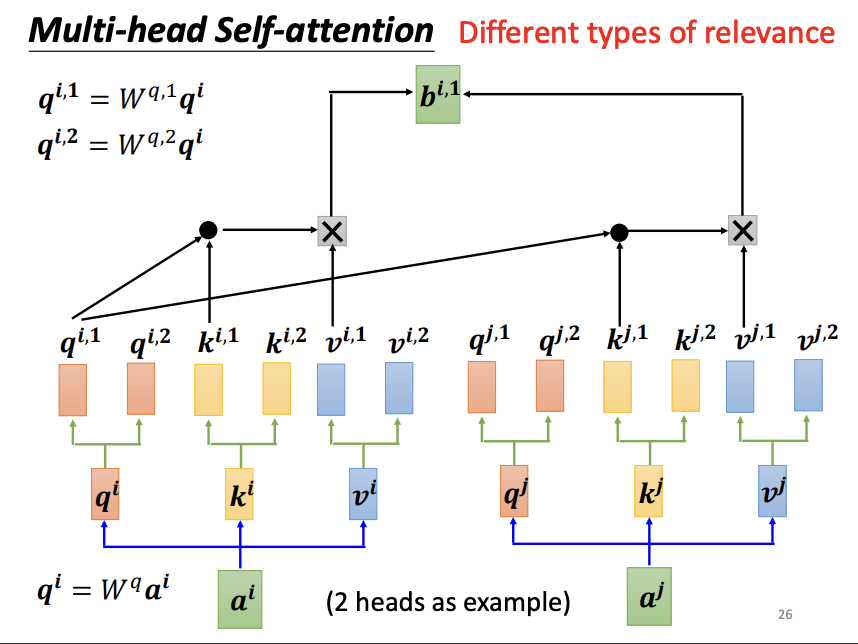
Multi-Head Self-Attention

Multi-head self-attention is an advanced variant of the self-attention mechanism that is widely used in modern architectures. The key insight behind multi-head self-attention is that relevance between vectors may exist in different dimensions. To capture these multi-dimensional relationships, multi-head attention employs multiple sets of query, key, and value matrices, allowing the model to attend to different aspects of the input simultaneously. The outputs from each “head” are then combined and passed through an output (O) matrix to produce the final result.

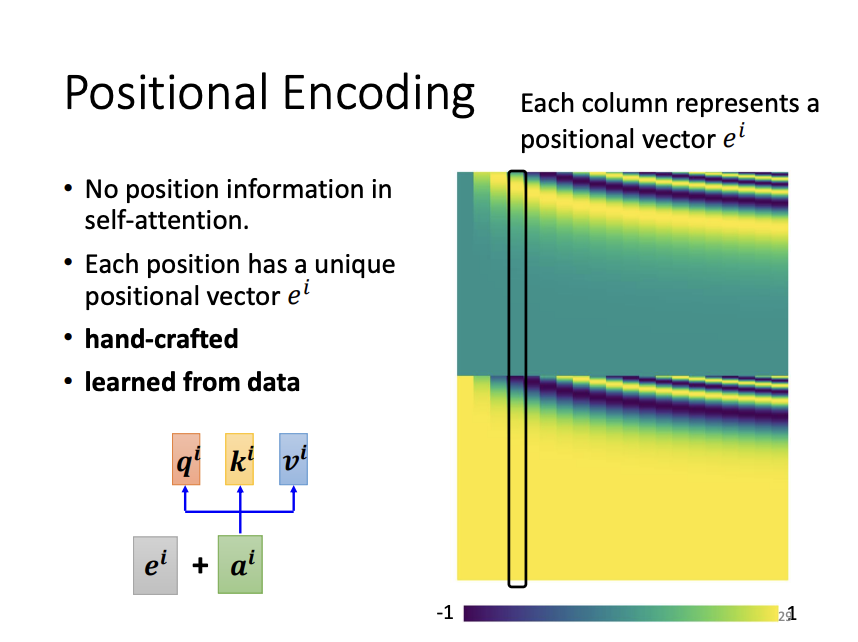
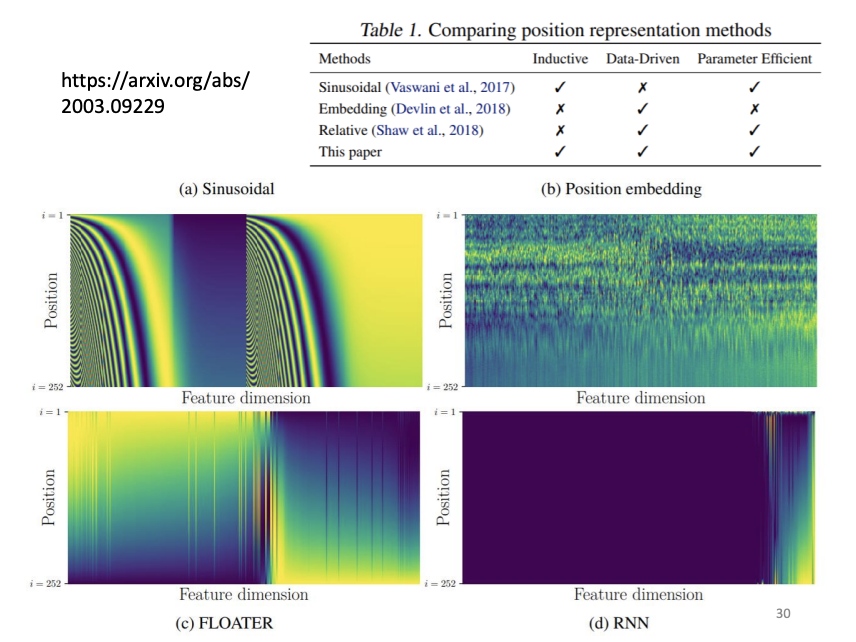
Positional Encoding

The basic self-attention mechanism does not inherently consider the order of the input vectors, which can be crucial in tasks where sequence structure is important. To address this, positional encoding is introduced. Positional encoding incorporates information about the position of each input vector by adding a unique positional vector to it. These positional vectors can either be hand-crafted or learned during training, enabling the model to capture sequential dependencies.

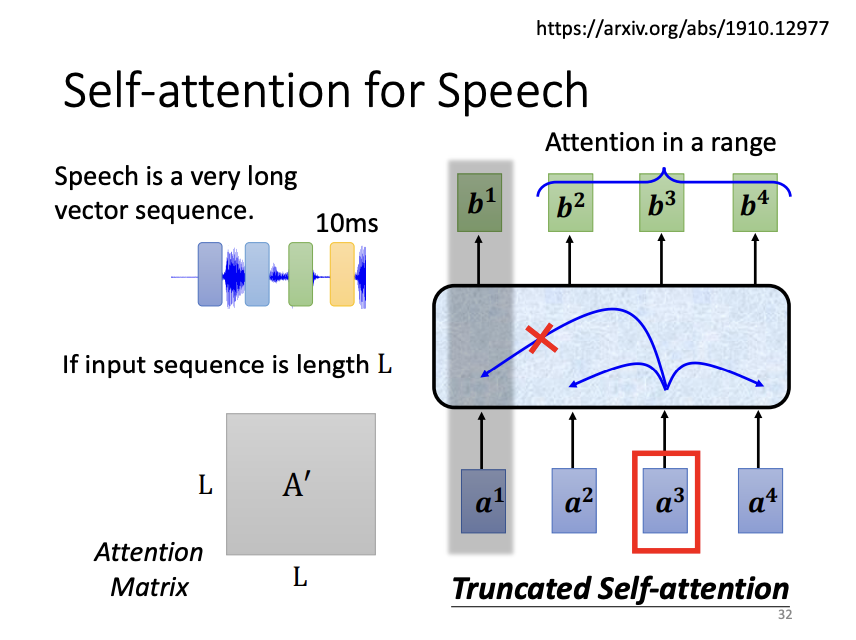
Application of Self-Attention

Self-attention has become integral to many state-of-the-art models, such as Transformer and BERT. In speech processing, self-attention can be applied with certain optimizations. Since speech signals consist of long vector sequences, they result in large attention matrices, which can be difficult to train. Truncated self-attention addresses this issue by limiting the attention to a range of nearby vectors, leveraging domain knowledge that the content of an audio signal is often only relevant to its immediate context.

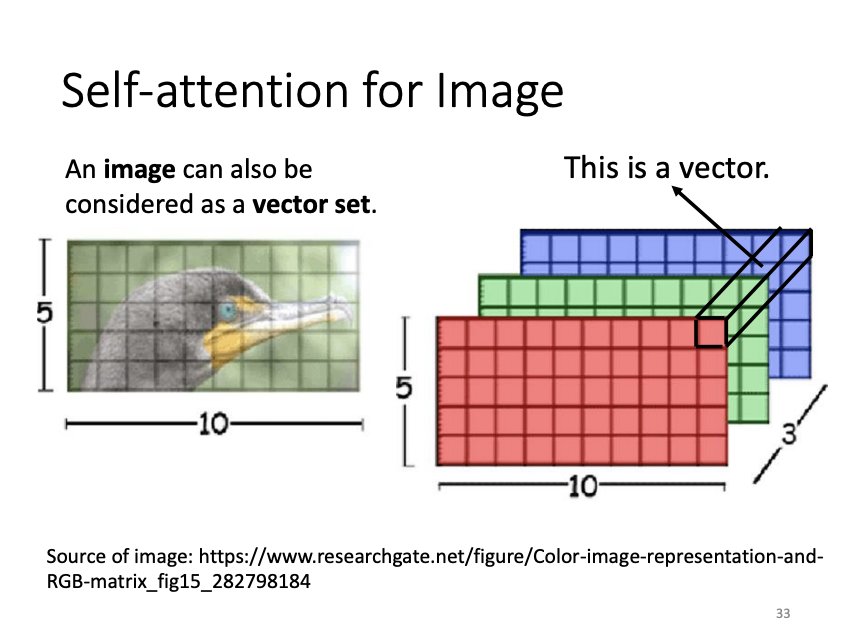
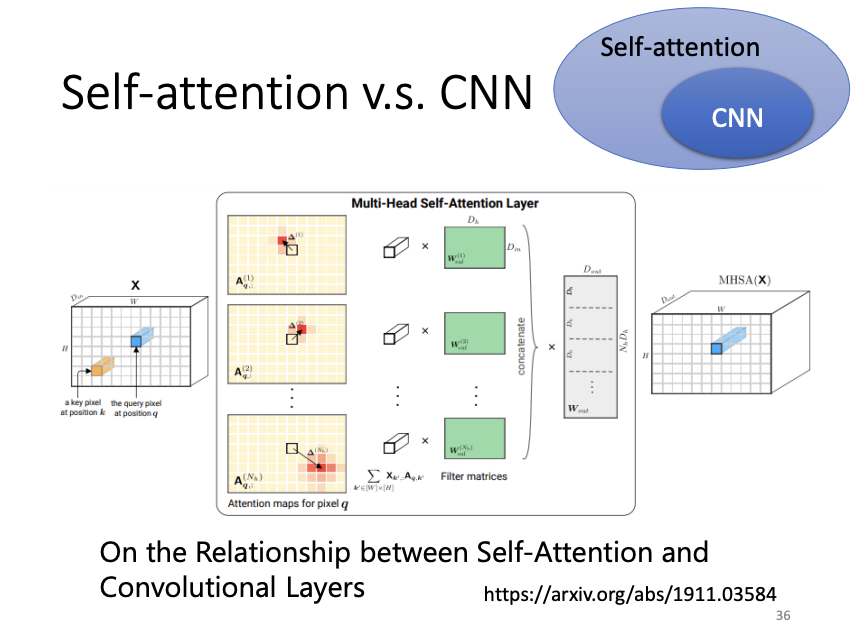
Self-attention can also be applied to image processing, where an image is treated as a set of vectors. Compared to convolutional neural networks (CNNs), self-attention is more flexible. While CNNs attend only to a fixed receptive field, defined by the user, self-attention dynamically attends to the relevant regions of the input based on learned attention scores. With appropriate parameter settings, self-attention can perform tasks similar to CNNs, but with greater adaptability.